0016-A-Knickstabilität vom einhüftigen Rahmen
Elisa Lafuente | Elisa Lafuente | Roland Sauer | Walter RustlerA0 Klassifikation
| Klasse | Analytisches Verifikationsbeispiel |
|---|---|
| Tragwerkstyp | Stabtragwerk |
| Mechanik | Statik-Theorie III. Ordnung |
| Materialgesetz | linear-elastisch |
| Baustoff | allgemein |
| Nachweisformat | Verformungsnachweis |
| Norm | keine Norm |
| Status |
veröffentlicht am 24.04.2018 und qualifiziert am 12.03.2019 |
A1 Problembeschreibung
Das zweidimensionale Rahmensystem wird mit einer Punktlast in A belastet. Durch Erhöhung der Punktlast verformt sich das System zunehmend bis Stabilitätsprobleme auftreten. Ziel des Beispiels ist es, das Last-Verformungs-Verhalten des Systems bis zum Erreichen des Knickpunkts zu berechnen. Verformungen sind nur in der XY-Ebene möglich.
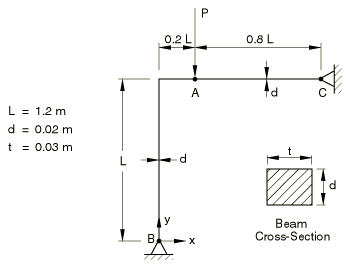
Material: linear-elastisch; E-Modul = 71740 MPa; Querdehnzahl = 0.0
Lagerung: ux = uy = 0 in B und C
Belastung: P = 1.0 kN
A5 Referenzen
[1] Lee, S-L.; Manuel, F.S.; Rossow, E.C., Large deflections and stability of elastic frames, in: Journal of Engineering Mechanics (ASCE) 94(EM2) (1968), 521–547.
[2] NAFEMS, Test NL7 from NAFEMS Publication NNB, Rev. 1, “NAFEMS Non-Linear Benchmarks”, Oktober: 1989.
[3] F. Gruttmann, R. Sauer, W. Wagner, A geometrical nonlinear eccentric 3D-beam element with arbitrary cross-sections, in: Computer Methods in Applied Mechanics and Engineering 160 (1998), 383-400.
Bearbeiten Referenzen
Löschen?
Möchten Sie dies wirklich löschen