0030-D-Interaktion Normalkraft Biegung
Casimir Katz | Casimir KatzD0 Classification
| Class | Design-Code-Based Verification Example |
|---|---|
| Type of structure | Other type of Structure |
| Mechanics | Other |
| Material law | Elastic-Plastic |
| Building material | Steel |
| Design type | Analysis of Ultimate Limit State (ULS) |
| Design code | DIN EN 1993 |
| Status |
published on 21-05-2021 |
D1 Problem description
Bei der plastischen Interaktion von Normalkraft und zweiachsiger Biegung wurde bislang in der Fachwelt keine einheitliche Meinung gefunden [1],[2],[3]. Strittig ist der Ansatz des Wölbmoments im plastifizierten Querschnitt.
Es geht um einen etwas vereinfachten HEB 200 und dessen Ausnutzung unter der kombinierten Beanspruchung von N=1000 kN, My=34.5 kNm und Mz=26.2 kNm.
Ein Wölbmoment ist als Beanspruchung nicht vorgegeben.
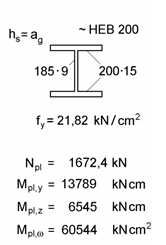
Die Aufgabenstellung umfasst die Ermittlung der Traglast unter dieser Schnittgrößenkombination an bis zu drei verschiedenen Systemen:
- Nachweis auf Querschnittsebene
- Nachweis mit einem FE-System (unter konstanten Momenten und Ebenbleiben der Querschnitte, also wölbfrei)
- Nachweis mit einem FE-System (Einfeldträger mit Länge von 2.0 m mit Gabellagerung und Lasteinleitung in Feldmitte)
D5 References
[1] Kindmann, R. Frickel, J., Grenztragfähigkeit von I-Querschnitten für beliebige Schnittgrößen, in: Stahlbau 4 (1999), 290-301.
[2] Rubin, H., Grundlage für N-My-Mz-Interaktionsbeziehungen von I-Querschnitten – Bernoulli oder Mb = 0?, in: Stahlbau 69 (2000), 807-812.
[3] Rubin, H., Das Tragverhalten von I-Trägern unter N-, My- und Mz-Beanspruchung nach Fließzonentheorie I. und II. Ordnung unter Berücksichtigung der Torsionseinflüsse. , in: Stahlbau 70 (2001), 846-856.
[4] Kindmann, R., Frickel, J., Elastische und plastische Querschnittstragfähigkeit, https://kindmann.de/downloads/file/2-elastische-und-plastische-querschnittstragfaehigkeit, 12-05-2021
[5] Katz, C., Fließzonentheorie mit Interaktion aller Stabschnittgrößen bei Stahltragwerken, in: Stahlbau 66 (1997), 205-213.
Edit References
Delete?
Are you sure you want to delete this