0006-A-Dünne Zylinderschale unter entgegengesetzt radial gerichteten Einzelkräften
Walter Rustler | Walter Rustler | Roland Sauer | Casimir KatzA0 Classification
| Class | Analytical Verification Example |
|---|---|
| Type of structure | Plate or Shell Structure-Shell |
| Mechanics | Statics-First-Order Theory |
| Material law | Linear-Elastic |
| Building material | General |
| Design type | Deformation Design |
| Design code | - |
| Status |
published on 03-08-2017 and qualified on 27-09-2018 |
A1 Problem description
Das System ist eine dünne Zylinderschale, die in ihrer Mitte durch zwei entgegengesetzt radial gerichtete Einzelkräfte belastet wird. Die Lagerung erfolgt ausschließlich an den Zylinderenden auf einer starren Kreisscheibe (nicht dargestellt), die eine Membranverschiebung erlaubt. In radialer Richtung sind die Verschiebungen damit an beiden Enden des Zylinders festgehalten. Es erfolgt keine Verdrehungsbehinderung. Untersucht wird die Durchbiegung in der Mitte des Zylinders unter einer der beiden Lasten in radialer Richtung für verschiedene Finite Element Netze. Das Beispiel erlaubt die Überprüfung der Eignung der Software zur Berechnung dünner Schalen mit regelmäßigen Netzen. Die geometrischen Angaben sowie die Materialangaben sind alle dimensionslos.
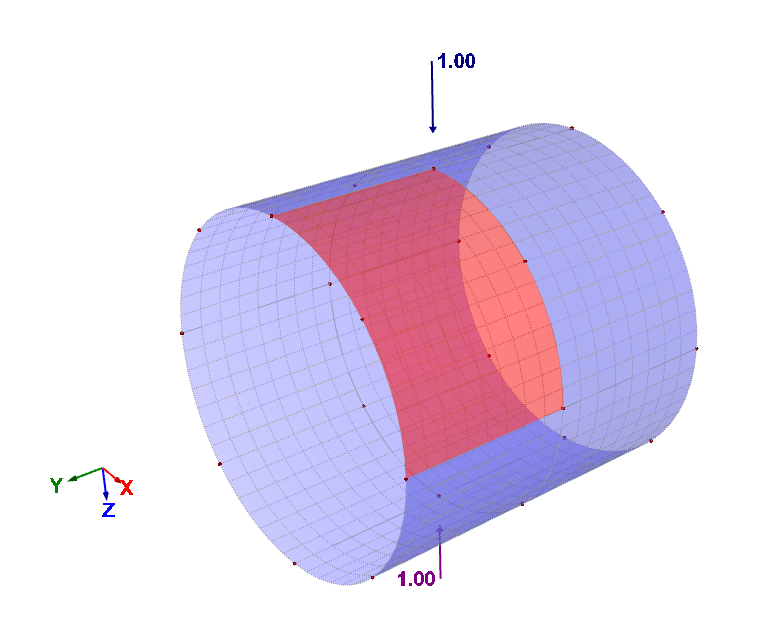
Bild A1.1: System
Systemabmessungen:
Schalenlänge l = 600,
Zylinderradius r = 300
Schalendicke h = 3.0
Material für Schale
Elastizitätsmodul E= 3.0 * 106
Querdehnzahl μ = 0.3
Randbedingungen:
An beiden Zylinderenden wird die Verschiebung lediglich in radialer Richtung behindert, wie dies bei der Anordnung von starren Kreisscheiben der Fall wäre, die gelenkig an den Zylinder angeschlossen sind. Diese Bedingung ist wesentlich, um das Biegeverhalten der Schale zu untersuchen. Wenn nur ein Viertel der Schale modelliert wird, sind an den geschnittenen Rändern Symmetriebedingungen anzusetzen.
Belastung:
Das Eigengewicht des Systems wird nicht automatisch berücksichtigt. Als Belastung werden radiale Einzellasten der Größe F = 1.0 in Schalenmitte entgegengesetzt gerichtet angesetzt. Bei einem Viertel des Systems ist dann nur F = 0.25 anzusetzen.
A5 References
[1] T. Belytschko, H. Stolarski, W.K. Liu, N. Carpenter and J.S.-J. Ong, Stress Projection for Membrane and Shear Locking in Shell Finite Elements, in: Computer Methods in Applied Mechanics and Engineering 51 (1-3) (1985), 221-258.
[2] ABAQUS , Theory Manual, Providence, RI, USA: Dassault Systèmes Simulia Corp. 2011, vers. 6.11.
[3] T.J.R. Hughes and T.E. Tezduyar, Finite Elements Based Upon Mindlin Plate Theory With Particular Reference to the Four-Node Bilinear Isoparametric Element, in: Journal of Applied Mechanics 48/3 (1981).
[4] G. Pimpinelli, An assumed strain quadrilateral element with drilling degrees of freedom, in: Finite Elements in Analysis and Design 41 (2004), 267-283.
Edit References
Delete?
Are you sure you want to delete this